Jeff Erickson 《Algorithms》04 -- 贪心算法

前言

　　在上一篇《动态规划》作者把贪心算法喷的一无是处，然而接着就是“真香”警告😹。本来想看作者怎么圆上一篇的发言，结果别人翻篇不提了。本文的内容不像前三篇那样环环相扣，而是独立的知识点。

知识点

磁带存储

假设我们有n个文件需要存储在磁带上。将来，使用者想要从这盘磁带上读取文件。从磁带上读取文件并不同于磁盘；首先我们要快进掉前面别的文件，那会耗费很多时间。用L[1..n]表示每个文件的长度；第i个文件的长度表示为L[i]。如果文件的存储顺序是1到n，那么查询第k个文件的耗费为

$$cost(k)=\sum\limits_{i=1}^kL[i]$$

这个耗费反映了实际上读取第k个文件之前我们必须浏览过所有之前的文件。如果假设每个文件被访问的概率相同，那么搜索一个随机文件的预期耗费是

$$E(cost)=\sum\limits_{k=1}^n\frac{cost(k)}{n}=\frac{1}{n}\sum\limits_{k=1}^n\sum\limits_{i=1}^kL[i]$$

　　如果我们改变磁带上文件的顺序，我们就改变了访问每个文件的耗费；有些文件的读取耗费会增大，但另一些的会变少。不同的顺序也会导致预期耗费不同。用π(i)表示第i个文件在磁带上的位置，那么关于排列π的预期耗费如下

$$E[cost(\pi)]=\frac{1}{n}\sum\limits_{k=1}^n\sum\limits_{i=1}^kL[\pi(i)]$$

　　如果我们想要预期耗费尽可能小应该怎样排序？凭直觉答案似乎很简单：按长度升序排列。但直觉是一头狡猾的野兽。只有一种方式可以确定这样排序能行，那就是证明它。
引理4.1. 对于所有i，当L[π(i)] ≤ L[π(i+1)]时，E[cost(π)]的值最小。
证明： 假设对于某个索引i，L[π(i)] > L[π(i+1)]。为了简化概念，让 a = π(i) 和 b = π(i+1)。如果交换a和b，那么访问a的耗费增加L[b]，访问b的耗费减少L[a]。总的来说，交换改变期望耗费的增量为(L[b]-L[a])/n。但是这个改变是一种优化，因为L[b]<L[a]。这样，如果文件不是顺序地，那就给它排个序。
　　这就是我们第一个贪心算法。为了最小化访问文件总共的预期耗费，我们把长度最短的文件放在开头，然后像这样依次写入别的文件；没有回溯，没有动态规划，只做最好的局部决定。
　　让我们更深入地分析这个想法。假设有一个数组F[1..n]，它表示每个文件的访问频率；第i个文件正好会被访问F[i]次。现在整个磁带所有文件被访问的耗费就是

$$\varSigma cost(\pi)=\sum\limits_{k=1}^n\big(F[\pi(k)]·\sum\limits_{i=1}^kL[\pi(i)]\big)=\sum\limits_{k=1}^n\sum\limits_{i=1}^k(F[\pi(k)]·L[\pi(i)])$$

和之前一样，对文件重新排序会改变总耗费。如果想好总耗费尽可能小应该怎样排序呢？
　　我们已经证明过同样频率的情况。如果频率不同但文件长度相同，那么凭直觉，我们应该按访问频率降序排列，访问次数最多的放在最前面。事实上，通过修改引理4.1来证明并不困难。但是如果文件长度和访问频率都不同的情况怎么办？这种情况，我们应该按照比例L/F来排序。
引理4.2. 对于所有i，当$\frac{L[\pi(i)]}{F[\pi(i)]}\leq \frac{L[\pi(i+1)}{F[\pi(i+1)]}$，$\varSigma cost(\pi)$的值最小。
证明： 假设对于某个索引i，L[π(i)]/F[π(i)] ＞ L[π(i+1)]/F[π(i+1)]。为了简化概念，用a = π(i) 和 b = π(i+1)。如果交换文件a和b，那么访问a的耗费增加了L[b],访问b的耗费减少了L[a]。总的来说，这个交换改变了总耗费的增量为L[b]F[a]-L[a]F[b]。但是这个改变是一种优化，因为

$$\frac{L[a]}{F[a]}＞\frac{L[b]}{F[b]}\Leftrightarrow L[b]F[a]-L[a]F[b]＜0$$

这样，如果两个相邻的文件不是按以上顺序，那就交换它们。

课程安排

接下来这个例子稍微复杂一点，假设学校为学生提供了一些课程选择，每节课开始和结束时间都不相同，并且不允许选择时间重叠的课程，如何参与最多的课程？
　　具体一点，假设给你两个数组S[1..n]和F[1..n]，分别表示每个课程的开始和结束时间；明确一下，对于每个i，都有$0\leq S[i] < F[i] \leq M$（M表示最晚课程结束时间）。你的任务就是找到X∈{1,2,3…,n}的最大子集，对于任意i,j ∈ X，满足S[i]>F[j]或者S[j]>F[i]。接着我们可以阐述这个问题，通过把每节课表示成一个矩形，矩形的左右两边的x坐标分别表示开始和结束时间，我们的目标就是一个在垂直方向上不重叠矩形的最大最大子集。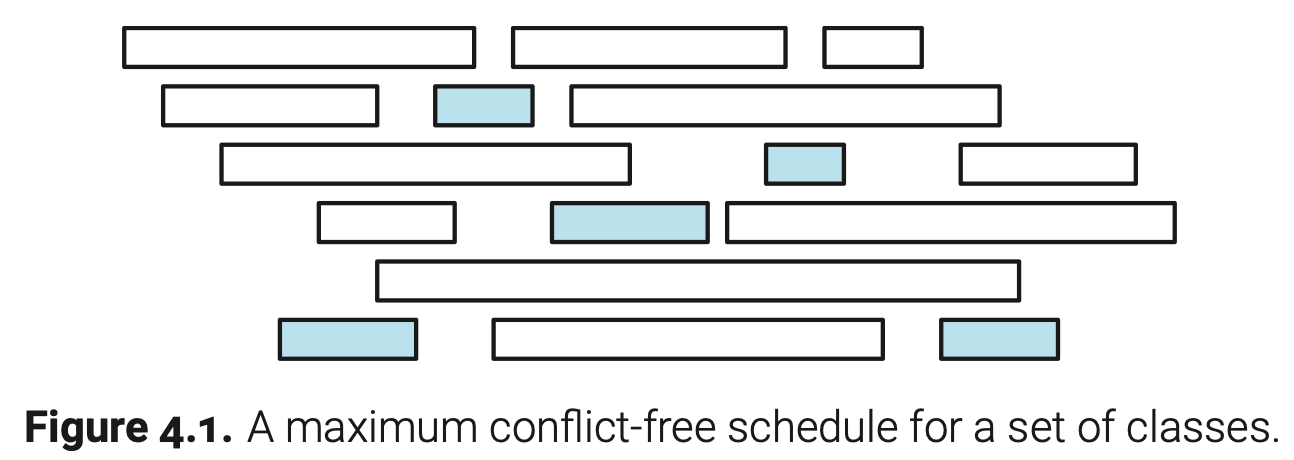

　　这个问题有一个相当简单的递归解法，基于是否选择第1节课。让B表示在第1节课开始之前就结束了的课程集合，用A表示在第1节课结束之后才开始的课程集合：

$$\begin{align}&B:=\{i|2\leq i\leq n\ and\ F[i] < S[1]\} \\ &A:=\{i|2\leq i\leq n\ and\ S[i]>F[1]\}\end{align}$$

如果第一节属于最佳安排，那么B和A中也存在最佳安排的课程。如果不是我们可以递归地在{2,3,…,n}中找到最佳安排课程。所以两种情况都要尝试，选择最好的那一个。自下而上地评估这个递归过程最后得到一个动态规划算法，运行时为$O(n^3)$。不用去思考具体怎么做，因为动态规划并不是这个问题的最优解法。
　　凭直觉我们希望第一节课的结束时间越早越好，因为这样做我们有更多的课程可供选择。这种直觉给了我们一个简单的贪心算法。通过结束时间的从早到晚遍历课程；如果当前课程与你上一次选择的课程不冲突，那就选择它。下图可以形象化表达弹性算法的过程：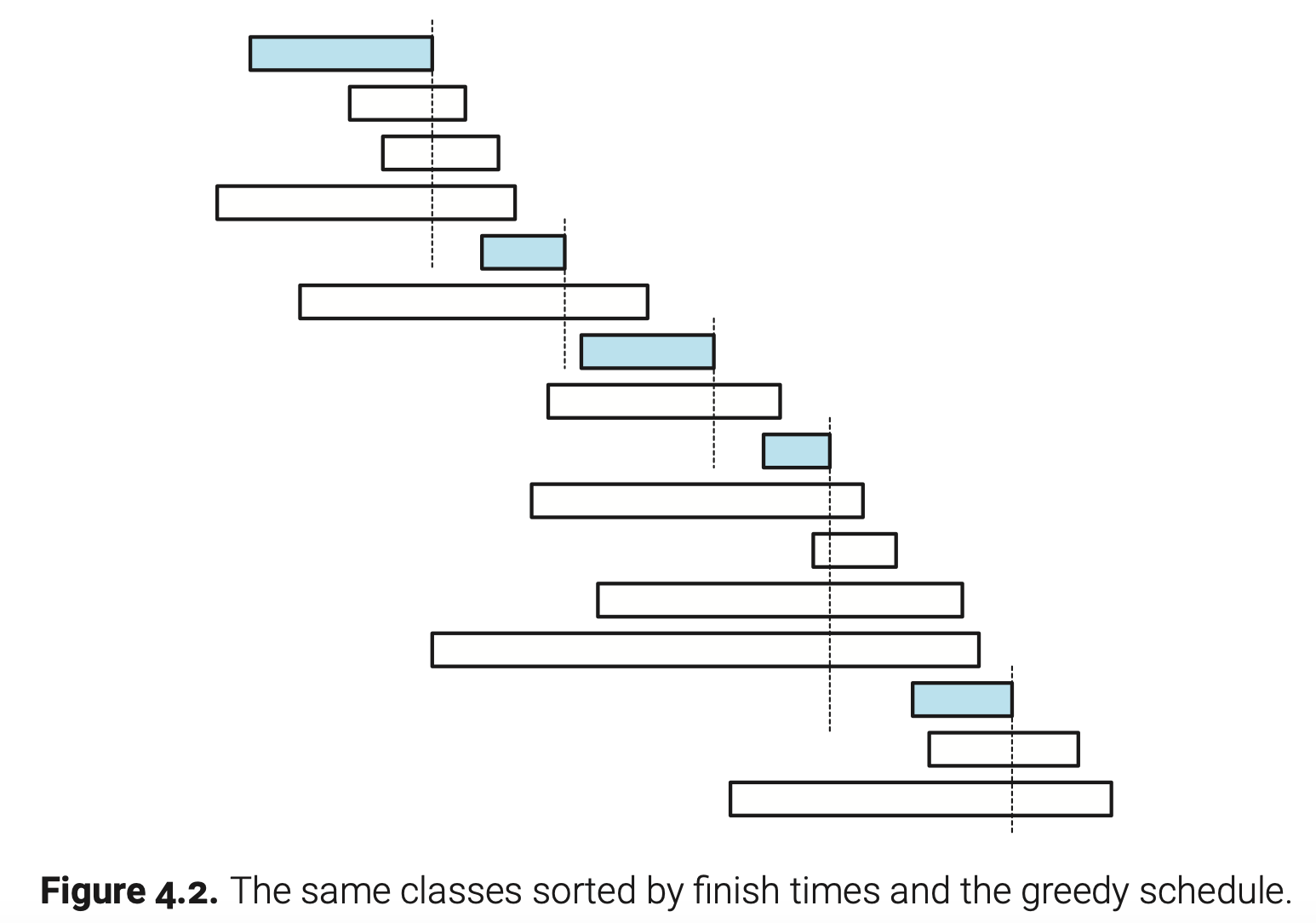

　　下面还有这个算法的伪代码。经过初始化排序，该算法就是一个线性时间的循环，所以它的运行时间是$O(n logn)$

　　为了证明这个算法计算出来的是一个最佳课程安排，我们使用交换论证法，就像前面磁带排序那种。我们不能说贪心算法找到的是唯一一种最佳课程安排；这可能有点让人疑惑（对比前面两张图你就知道了）。这里我们只能说贪心算法至少可以找到一种最佳课程安排。
引理4.3. 至少有一种最佳课程安排包含了最早结束的课程。
证明： 用f表示最早结束的课程。假设我们有一个最佳课程安排集合X，它不包含f。用g表示X中最早结束的课程。因为f比g结束的早，f就不可能和X\{g}冲突。因此，课程安排Y=X∪{f}\{g}也是一个不冲突集合。因为Y和X的大小相等，那么Y也是一个最佳课程安排。
　　接下来为了完成证明，我们要用到老朋友归纳法了。
定理4.4. 贪心算法计算出来的是最佳课程安排。
证明： 用f表示最早结束的课程，用A表示在f结束后开始的课程集合。上一条引理说明有一种最佳课程安排是包含f的，且这个安排的其他课程是不与f冲突的，那么这些其他课程也必然是A集合的最佳课程安排。贪心算法先选择了f，通过归纳假设，接着又计算A集合中的最佳课程安排。
　　如果我们稍微展开这个归纳法，这个证明看起来就会轻松一些。
证明： 用$\{g_1,g_2,…,g_{k}\}$表示贪心算法选择的课程序列，根据开始时间排序。假设我们有一个最佳课程安排

$$S=\{g_1,g_2,...,g_{j-1},c_j,c_{j+1},...,c_m\}$$

也是按开始时间排序的，$c_j$表示这个课程与贪心算法选择的课程$g_j$不同。根据算法规则，我们知道$g_j$是与$g_1,g_2,…,g_{j-1}$不冲突的，又因为集合S中的课程之间也是不冲突的，$c_j$也是。此外，$g_j$是与已选择课程不冲突且时间最早的一个；特别是$g_j$比$c_j$的结束时间早。这就表示$g_j$与后面的课程$c_{j+1},…,c_m$是不冲突的。因此，将课程安排修改成

$$S^{'}=\{g_1,g_2,...,g_{j-1},g_j,c_{j+1},...,c_m\}$$

也是不冲突的。（假设j=1,这个论证就包含了了定理4.3）
　　由归纳法可知，想要让最佳安排$\{g_1,g_2,…,g_k,c_{k+1},…,c_m\}$中的每一个课程选择都来自贪心算法，则必须有k=m；如果课程$c_{k+1}$与前k个贪心课程不冲突，那么贪心算法就能选出不止k个课程。

普遍模式

通过两个例子我们看出，正确性证明的基础结构是：归纳的交换论证。
　　• 假设有一种最佳方案不同于贪心方案。
　　• 找到两种方案首次出现不同的位置。
　　• 辩论我们是否可以通过交换两者中的不同选择，而且并没有让方案变差。
这个论证说明通过归纳法可知有一些最佳方案是包含了贪心方案的，而且它就是贪心方案。有时候，像在这种安排问题一样，我们需要一些额外的步骤证明没有别的方案可以优化贪心方案了。

霍夫曼编码

二进制编码是有0和1组成的一串数字。前缀二进制编码是一种二进制编码，它的任意编码不会成为其他编码的前缀。比如{1,11,111}这种编码就不是前缀二进制编码，因为1是11和111的前缀，11是111的前缀。
　　任意前缀二进制编码都可以形象化为一棵二叉树，编码字符都存储在叶子节点上。字符的编码就是从根节点到相应叶子节点的路径；往左表示为0，往右表示为1。这样，任意字符的编码长度就是对于叶子节点在编码树种的高度。尽管这看起来很相似，但是二叉编码树不同于二叉搜索树；我们并不关心字符在叶子节点中的顺序。
　　假设我们想要编码一段使用n个字符写出的信息，而且要越短越好。同时，又给出了字符使用次数的数组f[1..n]，我们想要计算出一段前缀编码而且编码长度还是最短的：

$$\sum\limits_{i=1}^nf[i]·depth(i)$$

　　这个看起来和之前最佳二叉搜索树的函数是一样的，但是也有不同之处，因为编码树只有叶子节点存储信息。
　　1951年，作为麻省理工学院的博士研究生，大卫·霍夫曼根据贪心算法发明了一个理想的编码规则：合并两个低频字符并且循环此步骤。
我们通过一个例子来了解算法，假设我们需要编码如下句子。

$$\begin{align}&THISSENTENCECONTAINSTHREEASTHREECSTWODSTWENTYSIXESFIVEFST\\ &HREEGSEIGHTHSTHIRTEENISTWOLSSIXTEENNSNINEOSSIXRSTWENTYSEV\\ &ENSSTWENTYTWOTSTWOUSFIVEVSEIGHTWSFOURXSFIVEYSANDONLYONEZ \end{align}$$

下面是句子中每个字符频率表格。

A	C	D	E	F	G	H	I	L	N	O	R	S	T	U	V	W	X	Y	Z
3	3	2	26	5	3	8	13	2	16	9	6	27	22	2	5	8	4	5	1

霍夫曼的算法就是从当前频率表格中选出使用最少的两个，然后把这两个合并成一个字符DZ，访问次数为3。原来的两个字符就从表格中移除，现在插入一个新的字符DZ。这个新的字符就成为了编码树中的内部节点（非叶子节点），它的子节点是Z和D。这个算法就是这样递归地合并字符，然后得到新的字符频率表格。

A	C	E	F	G	H	I	L	N	O	R	S	T	U	V	W	X	Y	DZ
3	3	26	5	3	8	13	2	16	9	6	27	22	2	5	8	4	5	3

经过19次合并后，所有20个字符都被合并成了一个。合并过程的记录就是我们的编码树。这个算法过程中有些决定是任取其一的，所有实际上是存在多种不同霍夫曼编码的。其中之一如下图所示；非叶子节点的数字代表合并后的字符访问频率。比如，字符A的编码是101000，字符S的编码是111。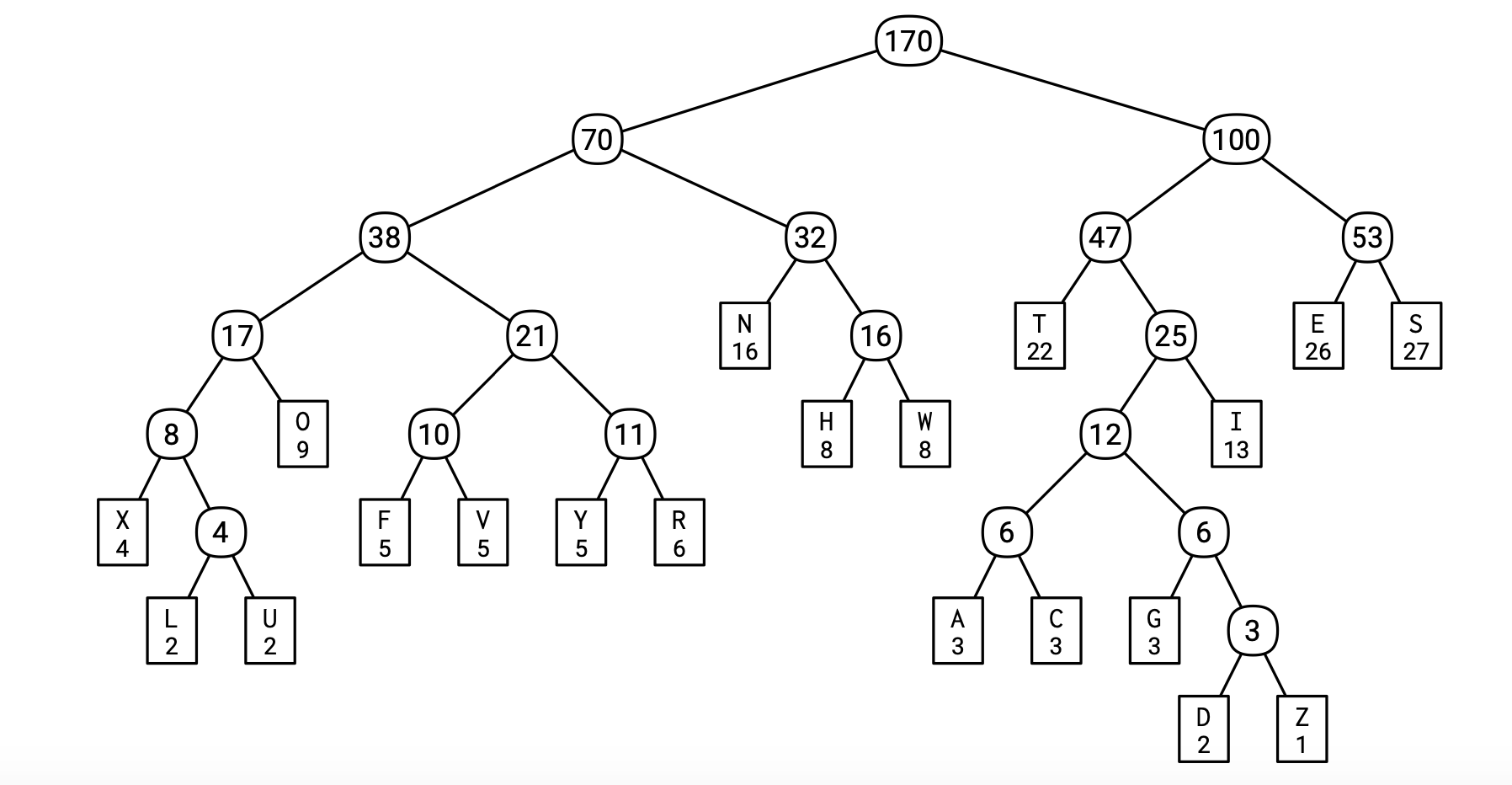

整个句子的编码过程如下：

$$\frac{100}{T}\frac{0110}{H}\frac{1011}{I}\frac{111}{S}\frac{111}{S}\frac{110}{E}\frac{010}{N}\frac{100}{T}\frac{110}{E}\frac{010}{N}\frac{101001}{C}\frac{110}{E}\ ····$$

根据每个字符的编码长度和使用次数，可以得出每个字符的编码总长度。

字符	A	C	D	E	F	G	H	I	L	N	O	R	S	T	U	V	W	X	Y	Z
频次	3	3	2	26	5	3	8	13	2	16	9	6	27	22	2	5	8	4	5	1
深度	6	6	7	3	5	6	4	4	6	3	4	5	3	3	6	5	4	5	5	7
总计	18	18	14	78	25	18	32	52	12	48	36	30	81	66	12	25	32	20	25	7

总共加起来得到编码信息的长度为649比特，不同的霍夫曼编码也会得到同样的编码长度。
　　通过给出的例子，我们并不惊讶它给出了最佳前缀编码。并且使用任何前缀编码编码前面的句子的最短长度都是649！但是接下来我们要证明，由于算法声明是递归结构的，我们可以使用前面提到的交换论证。我们从证明算法的每个初次选择是正确的开始。
引理4.5. 用x和y表示使用次数最少的两个字符。当x和y是兄弟节点时并且高度最大，存在一棵最佳编码树。
证明： 用T表示一棵最佳编码树，假设这棵树的深度是d。因为T是一棵满二叉树，那么它至少有两个叶子节点的高度为d，并且他们是兄弟关系。（归纳法可证明）假设这两个节点不是x和y，而是别的两个字符a和b。
　　用$T’$表示通过交换x和a之后的编码树，让$\Delta=d-depth_T(x)$。这个交换会增加x的高度$\Delta$并且减少a的高度$\Delta$，所以

$$cost(T')=cost(T)+\Delta·(f[x]-f[a])$$

我们的假设是x是两个最低频率字符之一但a不是，这表示$f[x]\leq f[a]$，并且我们假设了a的高度是最大的，这表示$\Delta\geq 0$。也就是说$cost(T’)\leq cost(T)$。又因为T是一棵最佳编码树，所以必须有$cost(T’)\geq cost(T)$。到此我们得出$T’$也是一颗最佳编码树。
　　同样的，交换y和b会得到另外一个最佳编码树，而且在最后这个最佳编码树种，x和y是高度最大的兄弟节点，如题所求。
　　现在算法的最佳性已经证明了。我们的递归论证基于一个非标准递归定义：一棵满二叉树要么一个单独的节点，或者是它的一些叶子被一个带有两个叶子的内部节点取代。
引理4.6. 每个霍夫曼编码都是一种最佳前缀二进制编码。
证明： 如果一段信息只由一个或者两个不同字符组成，那么证明起来很简单，所以假设其他情况。
　　让f[1..n]表示输入信息的字符频率表，为了不使普遍性假设f[1]和f[2]是两个低频字符。为了建立这个递归子问题，定义f[n+1]=f[1]+f[2]。这个操作就是把1和2两个作为f[1..n]某个最佳编码树中的高度最大的兄弟节点。
　　用$T’$表示f[3..n+1]的霍夫曼树；通过归纳假设我们知道$T’$就是最佳编码树的一部分。为了得到最终的编码树$T$，我们n+1所在的叶子替换成带有两个孩子的内部节点，它们非别是1和2。这里我们声明$T$是原频率数组f[1..n]的最佳编码树。
　　为了求证这个声明，我们使用$T’$来表达$T$的编码长度。

$$\begin{align}cost(T)&=\sum\limits_{i=1}^nf[i]·depth(i)\\&=\sum\limits_{i=3}^{n+1}f[i]·depth(i)+f[1]·depth(1)+f[2]·depth(2)-f[n+1]·depth(n+1)\\&=cost(T')+(f[1]+f[2])·depth(T)-f[n+1]·(depth(T)-1)\\&=cost(T')+f[1]+f[2]+(f[1]+f[2]-f[n+1])·(depth(T)-1)\\&=cost(T')+f[1]+f[2]\end{align}$$

这个方程表示优化$T’$和$T$的编码长度是等价的；特别是把$T’$的n+1节点粘上1和2作为叶子就得到了原频率数组的最佳编码树。
　　为了高效构造霍夫曼编码，我们将字符保存在优先队列中，使用字符使用频率作为优先级。我们使用三个数组下标来表示编码树，他们存储每个节点的左孩子、右孩子和父节点。编码树叶子节点的下标范围是1到n，根节点是2n-1。下图4.4中BuildHuffman函数执行$O(n)$次优先队列操作：恰好2n-1此时Insert和2n-2次ExtractMin操作。如果我们二进制堆来实现优先队列，每次操作执行时间为$O(log n)$，因此这个算法的运行时为$O(n log n)$。
　　最后，图中4.5的两个函数分别表示编码和解码；两个算法的运行时都是$O(m)$，m是编码后信息的长度。

稳定匹配

在美国每年都有大量临近毕业的医生需要到医院去实习，如何让医院和实习医生都彼此满意是一个让人头疼的问题。医生与医院存在一个双向选择问题，每个医生有自己喜欢的医院排名列表，而每个医院也有自己喜欢的医生排名列表。因此，一个叫做住院医师配对的项目（NRMP）因运而生。医生和医院互相递交自己的排名列表，NRMP会计算出一个医院和合生的配对名单并且满足接下来的稳定性要求。如果一个医生α和医院B都更倾向于选择对方而不满于当前匹配，那么当前的配对关系是不稳定的。比如
　　• 尽管α更喜欢医院B，但它与医院A配对了。
　　• 尽管B更喜欢医生α，但它与医生β配对了。
这种情况下，我们把(α,B)称作不稳定配对。而NRMP的目标是找到稳定匹配，这种表示匹配中不能存在不稳定的配对关系。
　　为了简化问题，假设现在医生和医院的数量是相同的；每个医院只提供一个实习岗位；每个医生对所有的医院做了排名；同样医院也对所有医生做了排名；最后，医生和医院之间的排名不存在非正当关系。

一些糟糕的思路

假设我们用小写字母代表医生，大写字母代表医院。有如下排名列表：

q	r	s		A	B	C
A	C	A		r	s	q
C	A	B		q	q	r
B	B	C		s	r	s

匹配{Aq,Br,Cs}是不稳定的，因为与q相比A更喜欢r，与B相比r更愿意在A工作。对于这个匹配来说，(A,q)是一个不稳定配对。
　　有人会想到使用增量算法来对任意匹配进行改进解决不稳定性。但是解决一个就可能创造另一个；事实上增量改进还可能导致无限循环，就用不稳定匹配{Aq,Br,Cs}来说：

$$\{Aq,Br,Cs\}\stackrel{Ar}{\longrightarrow}\{Ar,Bq,Cs\}\stackrel{Cr}{\longrightarrow}\{As,Bq,Cr\}\stackrel{Cq}{\longrightarrow}\{As,Br,Cq\}\stackrel{Aq}{\longrightarrow}\{Aq,Br,Cs\}$$

　　接着有人会试试多轮询（一次轮询表示一家医院对一个医生发出邀请）贪心。每一次循环，每一个未匹配医院对当前最心仪的未匹配医生发出邀请，每一个未匹配医生接受当前邀请中最喜欢的那家医院。不难证明每次循环都至少能决定一个配对，所以这个算法最终会得到一个匹配。对于前面的例子，仅仅一轮循环就得到了稳定匹配{Ar,Bs,Cq}。但是如果看路下面的输入：

q	r	s		A	B	C
C	A	A		q	q	s
B	C	B		s	r	r
A	B	C		r	s	q

在第一轮循环中，s接受了C的邀请，q接受了B的邀请（拒绝了A），只剩下r和A没有匹配了。因此两轮循环后多轮询贪心得到了匹配{Ar,Bq,Cs}。结果这个匹配并不稳定，因为A和s更倾向于选择彼此。

BostonPool和Gale-Shapley算法

1952年NRMP采用了Boston Pool算法，之所以这么命名是因为当初这个算法是在Boston区域被一个票据交换所使用。十年之后David Gale和Lloyd Shapley正式地分析概括这个算法并且证明它可以用来计算稳定匹配。于是这个算法开始广泛被采用。
　　Shapley和Alvin Roth因为他们对问稳定匹配的研究获得了2012诺贝尔经济学奖，后者获奖是因为他对于Shapley的研究推广和实际应用起到了至关重要的作用。（Gale没有获奖是因为他在2008年去世了）
　　和我们第一个失败的贪心算法一样，Gale-Shapley算法也是执行轮询直到每个岗位都被接受。每个循环包含两个步骤：
　　1. 任意一个未匹配医院A根据排名列表顺序对还未拒绝它的医生α发出一个邀请。
　　2. 如果α还未匹配，它会接受A的邀请。如果α已经配对但它更倾向于A，它可以拒绝当前配对接受A的邀请。否则，α直接拒绝邀请。
每个医生最后都会根据排名列表接受它收到的最好的邀请。简洁一点就是，医院贪心地发出邀请，医生贪心地接受邀请。其中医生可以拒绝当前配对并选择更好的邀请这一点是让这个彼此贪心策略有效的关键。假设有如下排名列表：

q	r	s	t		A	B	C	D
A	A	B	D		t	r	t	s
B	D	A	B		s	t	r	r
C	C	C	C		r	q	s	q
D	B	D	A		q	s	q	t

根据排名列表，Gale-Shapley算法会执行如下操作：
　　1. A对t发出邀请。
　　2. B对r发出邀请。
　　3. C对t发出邀请，t拒绝了A的邀请选择了C。
　　4. D对s发出邀请。（从这里开始只有一家医院还未匹配，所以算法没有太多选择了）
　　5. A对s发出邀请，s拒绝了D的邀请选择了A。
　　6. D对r发出邀请，r拒绝了B的邀请选择了D。
　　7. B对t发出邀请，t决绝了C的邀请选择了B。
　　8. C对r发出邀请，r拒绝了。
　　9. C对s发出邀请，s拒绝了。
　　10. C对q发出邀请。
在第十次轮询结束时，所有委决定的邀请都被接受了，算法得出了匹配{As,Bt,Cq,Dr}。你可以暴力验证这个匹配是稳定的，尽管没有医院雇用到了最喜欢的医生，也没有医生选择了最喜欢的医院；事实上，C最后雇用到了排名中最后的的医生。当然这个匹配不是根据排名列表得到的唯一稳定匹配；{Ar,Bs,Cq,Dt}也是稳定匹配。

运行时

一个医院最多对每个医生提出一次邀请，所有整个算法最多会提出$n^2$次邀请。为了分析实际运行时间，我们需要知道算法更多的细节。比如排名列表是怎么给到算法的？算法怎么判断一个医院是否是未匹配？算法怎么存储暂定匹配？最基本的：算法怎么表示医生和医院？
　　有一种表达方式就是使用1到n表示医院和医生。用两个数组Dpref[1..n,1..n]和Hpref[1..n,1..n]表示排名列表，Dpref[i,r]表示第r个医院在第i个医生排名列表中的位置，Hpref[i,r]表示第r个医生在第i个医院排名列表中的位置。用这个输入形式，Bostion Pool算法可以在常数级时间内执行邀请，经过一些初始化操作；整个算法的执行时间是$O(n^2)$。

正确性

但是为什么这个算法是正确的呢？我们怎么知道这个算法总是能计算出稳定匹配，或者计算结果有可能仅是一个完全匹配？
　　一旦一个医生接受了邀请，它在剩下的时间内至少会有一个暂定配对。同样的，如果一个医生是未匹配的，那么就没有医院对它发出过邀请，这就表示医院还没有耗尽它的排名列表。当算法结束的时候，每个医生都是已匹配的，同样每个医院的职位都是已聘用的。换句话说，算法总是会得出一个医院和医生的完全匹配。剩下的就是要证明这个匹配是稳定的。
　　假设算法将医生α和医院A配对，尽管α更心仪医院B。因为每个医生只接受收到过的最好邀请，这表示α接受过的最好邀请来自A；有可能B没有邀请过α。也就是说，B对所有排名超过β的医生都发出过邀请。这就表示与α相比B更喜欢β，这意味着(α,B)不是稳定配对。最后我们得出结论：算法得出的匹配不存在不稳定配对；它是稳定的！

最佳性

令人惊讶的是Gale-Shapley算法的正确性并不依赖于哪个医院在每轮做出的邀请。事实上，不管哪个未分配的医院在每次轮询做出邀请，这个算法总是可以计算出相同的匹配！如果一个稳定匹配将医生α分配给医院A，对于医院A来说α是一个合适的医生。
引理4.7. 在Gale-Shapley算法执行过程中，每个医院A都会被对于A不合适的医生们拒绝。
证明： 我们对执行轮询的次数使用归纳法。假设在某一次轮询中，医生α拒绝医院A选择了医院B。这个拒绝表示与A相比α更倾向于B。在B的排名列表中优先级高于α的医生都已经在前面的轮询中拒绝了B，因此通过归纳假设可以知道这些医生都不适合B。
　　现在考虑一个任意匹配（对于相同的医院和医生），将α分配给A。我们已经知道与A相比α更倾向于B。如果与当前配对相比B更喜欢α，这个配对是不稳定的。另外如果与α相比B更乐于接受当前配对，那么当前配对的医生是不合适的（前面的论证有说明），也说明这个匹配是不稳定的。这里得出的结论就是将α分配给A的匹配不是稳定匹配。

　　现在用best(A)表示最适合A的医生。引理4.7表示医院A在最终匹配之前邀请过的医生都是不合适的。另一方面，最终匹配是稳定的，所以分配给医院A的医生必须是合适的。那么接下来的推论就是很明显的：
推论4.8. Gale-Shapley算法为每个医院A都匹配到了best(A)。

　　换句话说，Gale-Shapley算法站在医院的角度计算出了可行的最好稳定匹配。也就表示这个匹配对于医生来说应该是可行的最坏选择！用worst(α)表示医生α的最差可选的医院。

推论4.9 Gale-Shapley算法为每一个医生α都匹配到了worst(α)。
证明： 假设Gale-Shapley算法把医生α分配到了医院A；我们需要证明A=worst(α)。如果有任意一个稳定匹配存在A没有与α配对而是β。前面的推论告诉我们跟β相比A更喜欢α=best(A)。由于这个匹配是稳定的，因此α应该更喜欢它被分配的医院而不是A。这个论述对任何稳定匹配都是有效的，所以α更愿意选择别的可行匹配而不是A；换句话说，A=worst(α)。

　　1981年Lester Dubins和David Freedman发现了这两个推论会造成一些微妙的后果，那就是医生可以通过谎报排名列表来优化自己的配对情况，而医院却不行。出于这方面的原因，在1998年NRMP颠倒了匹配算法的选择关系，那就是医生根据排名对医院发出合作请求，医院则根据排名列表接受收到的最好合作请求。这样，新的算法计算出了对医生最优可行选择的匹配，自然医院就是相反的情况。然而实际上这个关系颠倒只改变了不到1%的匹配情况。

结语

起初我做jeffe教授的文章翻译就是为了记录知识要点。但现在我对一些有趣知识点的背景故事也进行了翻译，大概是怕自己以后读起来太枯燥了吧。稳定匹配的背景故事比较有趣，没想到医院招聘还有这段历史。至于霍夫曼编码这个知识点，我在一些讲文件压缩的文章中读到过，现在也算是加深印象了。
　　谈谈我自己对贪心的看法吧。遇到任何问题，我觉得最容易想到的思路就是贪心，同时它也是最容易被错用的算法。对比贪心和动归两篇文章的普遍模式小节，我发现贪心的套用模步骤简短而且模糊，也就是贪心这个方案用起来很灵活，在正确性验证方面可能不太好找切入点；而像动归这种套用模式详细的算法用起来反而更稳当，也比较好验证。

原文链接

http://jeffe.cs.illinois.edu/teaching/algorithms/book/04-greedy.pdf